现时， 千般在线酬酢汇集应用的快速发展积贮了多半的图数据.图数据由节点和边组成国产传媒， 且节点之间往往存在复杂的集结关系， 时常枯竭显式的全序结构， 使得图排序(graph ranking)成为图数据挖掘、分析的伏击技能[1].

PageRank[2]是图中节点伏击性度量的常用方法， 其基本想想是:节点伏击性由其络续节点伏击性决定， 被伏击节点集结的节点， 伏击性越高.一般来说， PageRank值度量了图中节点的全局伏击性或巨擘度， 但PageRank值却不成很好地度量图上节点间的相似性.为此， 筹商者进一步淡薄了个性化PageRank(personalized PageRank， 简称PPR)[3].但如文件[4， 5]指出:在使用PPR方法进行相似性查询时， 其复返的top-k轨则只筹商查询关联性(relevance)而忽略了千般性(diversity).然则在骨子图排序应用环境中， 用户的查询意图很难准确描画， 往往具有不细目性、隐隐性以及多义性.因此， PPR方法仍不成很好地安静图排序应用的要求.

当用户信得过的查询意图难以准确获取时， 对查询轨则进行千般性处理， 是信息检索系统处理此贫寒的灵验方法[6].为提供高质地的查询轨则， 提高用户查询的惬意度， 淡薄大概灵验折中关联性和千般性的图排序算法， 是图数据挖掘、分析规模面对的筹商挑战.为此， 连年来许多学者淡薄了一系列的千般性图排序方法[4， 5， 7-10].

当今， 已有的千般性图排序方法主要分为以下两类.

(1) 基于优化的方法[7-9].

国产久v久a在线观看视频

这一类方法通过诞生方向函数来刻画关联性和千般性， 并将问题建模为该方向函数的优化问题， 进而淡薄相应的优化算法.代表性责任有:Tong等东谈主[7]淡薄一个方向函数， 不错在筹商节点中心度和千般性的条目下空洞评价集结的质地， 但是该方向函数莫得筹商图数据固有的拓扑结构特征， 不成很好地处理千般性图排序的评价问题.Li等东谈主[8]将千般性图排序建模为一个双方向优化问题， 其中， 用排序轨则集的PPR值之和算作关联性度量， 并淡薄膨大率(expansion ratio)来度量排序轨则的千般性.Kucuktunc等东谈主[9]编削了文件[8]的责任， 将关联性和膨大率进行和会， 进一步淡薄了膨大关联性(expansion relevance)来度量排序轨则的千般性.上述方法千般性度量目的不尽疏导， 但最终的方向函数均施展为非负、单调的子模函数(submodular function).因此， 固然千般性图排序问题是NP-hard的， 但采用贪默算法可在多项式时间近似求解该问题;

(2) 基于就地游动的方法[4， 5， 10].

就地游动是度量图上节点伏击性的灵验方法， 然则惯例的就地游动方法未筹商节点之间的集结关系， 因此排序轨则千般性差.为此， 关联学者淡薄了编削的就地游动方法来增强排序轨则的千般性.代表性的筹商责任有DivRank[4]、GSparse[5]、GrassHopper[10].这类方法在就地游动经过中充分筹商了节点间的集结关系， 通过引入节点间的竞争机制， 让相互相连的节点相互竞争， 已毕排序轨则的千般性.然则， 这类方法要么计较成果低， 难以适用于大限制汇集， 要么枯竭明确的优化方向， 不具备可解释性[1].

综上， 面对大限制图数据的千般性图排序责任， 在优化方向、计较成果方面仍存在筹商挑战.具体地:

领先， 千般性度量目的是千般性图排序建模的中枢问题.文件[8]淡薄了膨大率度量千般性， 文件[9]将关联性和千般性进行和会， 进一步淡薄膨大关联性.骨子上， 膨大关联性即是一种以节点PPR值为权重的带权膨大率.采用膨大率或者膨大关联性对千般性进行建模的基本想想是:轻易两个节点的共同邻居越少， 两个节点越不相似.节点集合， 节点间不相似进度越高， 则节点集的膨大率或者膨大相似性越大.然则， 膨大率和膨大关联性的界说并非获胜基于结点间的不相似性来描画节点集的千般性.换言之， 具有高膨大率或高膨大关联性的节点集， 其里面节点间的不相似性巧合高.

底下例如阐发此问题.先给出膨大率的花样化描画[8].令G= < V， E > 是一个图， 其中， V是节点集， E边集.令S⊆V是图上的轻易节点集.N(S)是S的膨大集， 即N(S)=S∪{v∈(V-S)|$\exists $u∈S， (u， v)∈E}， 那么S的膨大率界说为er(S)=|N(S)|/|V|.如图 1所示:图 1(a)、图 1(b)子图中， 节点集S={1， 2}的膨大集均为N(S)={1， 2}∪{3， 4， 5， 6}， 由膨大率界说可知， 两个子图中S的膨大率均为er(S)=|N(S)={1， 2， 3， 4， 5， 6}|/|V={1， 2， 3， 4， 5， 6}|=1.然则， 图 1(a)中节点1与节点2具有疏导邻居， 节点1和节点2应具有高度相似性.图 1(b)中的节点1与节点2无共同邻居， 应不相似.因此， 膨大率或者膨大关联性无法灵验度量图 1所示情形中节点之间的不相似性， 进而无法灵验度量结点集的千般性.

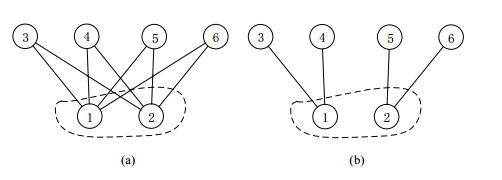Fig. 1 Illustration of deficiency of expansion ratio on measuring dis-similarity between two nodes 图 1 基于膨大率度量节点间的不相似性的不及之处

其次， 已有的基于优化的方法均将千般性图排序建模为一个基数管理下的非负、单音调模函数最大化问题.该问题是NP-hard的， 可采用贪默算法近似求解[11].算法从空的解集运行， 每次迭代时， 考中具有最大旯旮孝敬的节点加入到现时解集合.关于含m个节点的查询关联集来说， 为获取top-k排序轨则， 需要进行O(mk)次旯旮孝敬评估.当对大限制图数据进行千般性图排序时， 计较代价高， 算法的可膨大性成为很大的挑战.此外， 由于贪默算法的实行经过是一个串行迭代经过， 已有方法很难充分欺骗诸如Spark GraphX[12]等图数据计较平台进行高效并行计较.

于是， 关于千般性图排序筹商， 本文淡薄两个问题:能否淡薄基于节点间不相似性的节点集千般性度量目的?基于此度量目的淡薄的千般性图排序问题能否得到高效求解?

针对这两个问题， 领先， 淡薄了一种基于节点络续信息的节点间不相似性的度量目的， 并施展了该度量是节点间的一种距离度量(distance metric)， 即该度量安静非负、对称以及三角不等式等性质.基于该距离度量， 将千般性图排序建模为一种带权都备图上的组合优化问题.具体地， 以PPR查询节点组成节点集， 以节点间的距离度量算作边权重构造带权都备图.求解top-k千般性图排序轨则归结为求解该带权都备图的含k个结点的最大权子图.尽管该问题被施展是NP-hard的， 收成于边权重安静距离度量性质， 淡薄了多项式时间的2-近似算法求解该问题.此外， 由于带权图上不同节点对的距离度量计较是相互寥落的， 进而淡薄了基于GraphX的并行化算法.临了， 在信得过图数据集上， 将本文方法与已有方法在算法实行时间、关联性以及千般性上进行了对比测试， 本质轨则考证了本文疏辽阔法的灵验性.

本文第1节给出节点间不相似性的距离度量界说， 进而给出基于此距离度量界说的千般性图排序问题模子.第2节给出千般性图排序的(并行化)求解算法.第3节给出本质轨则.第4节记挂全文并接洽翌日的责任.

1 问题建模

本节中， 先诞生节点间不相似性的距离度量.基于此距离度量， 将千般性图排序问题建模为一种带权都备图上的组合优化问题.

1.1 节点间的距离度量

节点间不相似性的度量顺序是千般性图排序的基本问题.本文所谋划的千般性图排序问题不触及图或边的属性信息， 因此， 节点的邻居节点集成为界说节点间不相似性的伏击依据.直不雅地， 两个节点的非共同邻居越多， 则节点间的不相似进度越高.若是筹商到节点的PPR值， 那么节点间非共同邻居的PPR值之和越大， 则节点之间越不相似.基于上述不雅察， 节点的非共同邻居集可算作节点间不相似性的度量基础.于是， 令f是界说在节点集上的函数， 基于f可诞生图G上轻易两节点v， u之间的不相似度df(v， u).

界说1.  令G= < V， E > 是一个图， N(v)是节点v的邻居集.∀v， u∈V， 基于函数f的不相似度记为df(v， u)， 并界说:

$ {d_f}\left( {v， u} \right) = f(N\left( v \right) \oplus N\left( u \right)) $ (1)

其中， ⊕是集结间对称差运算， 具体含义为:给定轻易2个集结A， B， A⊕B=(A-B)∪(B-A).

在进一步谋划df(v， u)前， 先给出v， u之间距离度量的界说.

界说2.  令df(v， u)是v， u间的不相似度若df(v， u)安静底下3条性质， 则称df(v， u)为v， u间的一种距离度量[13].

(a)    df(v， u)安静非负性， 即df(v， u)≥0;

(b)    df(v， u)安静对称性， 即df(v， u)=df(u， v);

(c)    df(v， u)安静三角不等式， 即∀v， a， u⊆V， df(v， u)≤df(v， a)+df(a， u).

由上述界说可知， df(v， u)的含义和性质决定于函数f.底下施展:若是f是节点集上的权重和函数， 则由f决定的df(v， u)是v， u间的一种距离度量.

定理1.令A⊆V是轻易节点集， w(v)∈$\mathcal{R}$+是节点的非负权重.令f是节点权重和函数， 即$f(A)=\sum\limits_{v\in A}{w(v)}$ ， 并记$W=\sum\limits_{v\in V}{w(v)}$ .那么由f决定的不相似度是v， u间的一种距离度量.

$ {d_f}(v， u) = f(N(v) \oplus N(u)) = \sum\nolimits_{v \in N(v) \oplus N(u)} {(w(v)/W)} $ (2)

施展:设v， a， u是V集合轻易3个节点， 关于轻易节点v， 其邻居节点集记为N(v).为简化记号， 设N(v)=X， N(a)=Y以及N(u)=Z.按照界说2， 从以下3个方面分袂进行施展.

(a) df(v， u)安静非负性， 即df(v， u)≥0.由界说1可知， df(v， u)=f(X⊕Z).由于f是节点集上的非负权重和函数， 故f(X⊕Z)≥0， 于是df(v， u)≥0;

(b) df(v， u)安静对称性， 即df(v， u)=df(u， v).df(v， u)=f(X⊕Y)， 且df(u， v)=f(Y⊕X).⊕安静运算交换性， 因此， f(X⊕Y)= f(Y⊕X).于是， df(v， u)=df(u， v);

(c) df(v， u)安静三角不等式.

要施展df(v， u)≤df(v， a)+df(a， u)， 等价于施展f(X⊕Z)≤f(X⊕Y)+f(Y⊕Z).因为X⊕Z⊆(X⊕Y)∪(Y⊕Z)， 且f是单调非递减函数， 咱们有:

$ f(X \oplus Z) \leqslant f((X \oplus Y) \cup (Y \oplus Z)) $ (3)

又因为f短长负权重和函数， 因此关于轻易节点集A， B， C， 均有f(A∪B)≤f(A)+f(B).于是:

$ f((X \oplus Y) \cup (Y \oplus Z)) \leqslant f(X \oplus Y) + f(Y \oplus Z) $ (4)

空洞式(3)、式(4)可得:

$ f(X \oplus Z) \leqslant f(X \oplus Y) + f(Y \oplus Z) $ (5)

于是， df(v， u)≤df(v， a)+df(a， u).

综上情形(a)~情形(c)， df(v， u)是节点间的一种距离度量.

基于界说1、定理1的论断， 界说图上节点之间的距离度量如下.

界说3.  令r是个性化PageRank的排序值向量， r(v)∈$\mathcal{R}$+是v的PPR值， $f(A) = \sum\limits_{v \in A} {\boldsymbol{r}(v)} $为节点集A的PPR值之和， 并记R=f(V)， 则可界说节点v， u之间的距离度量df(v， u)如下:

$ {d_f}(v， u) = f(N(v) \oplus N(u)) = \sum\limits_{v \in N(v) \oplus N(u)} {(\boldsymbol{r}(v)/R)} $ (6)

底下给出df(v， u)的示例.图 2给出一个节点带权有向图， 设节点权值为PPR值， 由公式(6)可得:

$ {d_f}(2， 5) = \sum\limits_{v \in N(2) \oplus N(5)} {(\boldsymbol{r}(v)/R)} = \sum\limits_{\{ 2， 4， 5， 6， 7， 10， 11\} } {(\boldsymbol{r}(v)/R)} = 0.574. $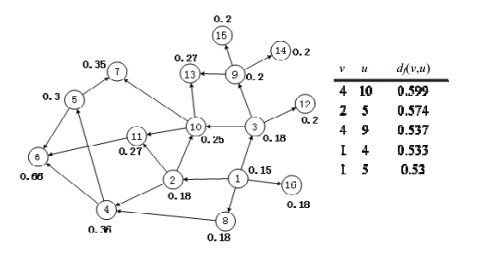 Fig. 2 Demostration of distance metric between nodes 图 2 节点之间距离度量计较示例

图 2还给出了有向图上距离值最大的前5对节点相等距离值.

1.2 问题模子

千般性图排序问题需要界说关联性、千般性度量.先谋划关联性度量， 然后基于第1.1节间节点的距离度量界说千般性度量， 临了将千般性图排序建模为带权都备图上的优化问题.

领先谋划关联性度量.个性化PageRank是图数据上已毕关联性查询的灵验方法[3].具体地， 令G是一个包含n个节点的图.节点的个性化PageRank排序向量可由如下迭代公式计较:

$ \mathit{\boldsymbol{r}} = \alpha \mathit{\boldsymbol{A'r}} + (1 - \alpha )\mathit{\boldsymbol{q}} $ (7)

其中， α(0 < α < 1)为阻尼因子; A是一个行标准化的图络续矩阵， 即$\sum\nolimits_{j = 1}^n {\boldsymbol{A}(i， j)} = 1， i = 1， 2， ...， n$.给定查询向量q(n×1的列向量$\boldsymbol{q}(i) \geqslant 0， \sum\nolimits_{i = 1}^n {\boldsymbol{q}(i)} = 1$)， 公式(7)会不断到节点集V上的一个巩固散布， 此散布即为排序值向量r.关于轻易结点v∈V， r(v)度量了v与q的相似性.于是， 给定一个排序轨则S， 可用S的排序值之和， 即$rel(S)=\sum\nolimits_{v\in S}{\boldsymbol{r}(v)}$度量关联性.

其次， 如第1.1节谋划， df(v， u)给出了节点v， u间的一种距离度量.

于是， 可用S中节点间的距离度量和$div(S)=\sum\nolimits_{v， u\in S}{{{d}_{f}}(v， u)}$度量其千般性.

给定查询向量q， 令Q⊆ V是查询关联节点集， 即∀v∈Q， 有r(v) > 0.界说优化方向函数F(S)如下:

$ F(S)=rel(S)+\lambda div(S)=\sum\limits_{v\in S}{\boldsymbol{r}(v)}+\lambda \sum\limits_{v， u\in S}{{{d}_{f}}(v， u)} $ (8)

其中， λ(0 < λ < 1)是折中因子， 用来折中关联性和千般性.若是|S|=k， 看重到:公式(8)中， rel(S)为k项r(v)之和.同期， div(S)为k(k-1)/2之和.为均衡rel(S)与div(S)， 分袂与不同的因子相乘， 于是改写F(S)为底下的公式(9):

$ F(S) = (k - 1)\sum\limits_{v \in S} {\boldsymbol{r}(v)} + 2\lambda \sum\limits_{v， u \in S} {{d_f}(v， u)} $ (9)

于是， Topk千般性图排序问题(TopkDRG)可界说为

$ {S^*} \leftarrow \arg {\max _{S \subseteq Q \subseteq V， |S| = k}}F(S) $ (10)

底下施展由公式(10)界说的TopkDRG是NP-hard的.

定理2.  令G= < V国产传媒， E > 是一个图， 则图G上的TopkDRG问题是NP-hard的.

施展:在图G上给定查询向量q， Q是q的查询关联节点集.引入如下和会节点关联性和不相似性的距离度量， 记为${d'_f}(v， u).$

$ {d'_f}(v， u) = \boldsymbol{r}(v) + \boldsymbol{r}(u) + 2\lambda {d_f}(v， u) $ (11)

不难考证， ${d'_f}(v， u)$仍然安静界说2中所述距离度量的非负、对称、三角不等式3条性质.

令${D'_f}(S) = \sum\nolimits_{v， u \in S} {{{d'}_f}(v， u)} $为节点集S中统统节点对的度量距离和， 由公式(11)可知:

$ {D'_f}(S) = \sum\limits_{v， u \in S} {{{d'}_f}(v， u)} = (k - 1)\sum\limits_{v \in S} {\mathit{\boldsymbol{r}}(v)} + 2\lambda \sum\limits_{v， u \in S} {{d_f}(v， u)} = F(S). $

也即是说， TopkDRG的方向函数F(S)等于节点集S中节点对的${d'_f}(v， u)$度量距离之和， 即TopkDRG可描画为

$ {S^*} \leftarrow \arg {\max _{S \subseteq Q \subseteq V， |S| = k}}F(S) = \arg {\max _{S \subseteq Q \subseteq V， |S| = k}}{D'_f}(S) $ (12)

至此， 以Q集为节点集、以${d'_f}(v， u)$为Q中节点v， u之间的边权重构造了带权都备图C(Q).由公式(12)可知， TopkDRG等价于在带权都备图C(Q)上求解包含k个节点的最大边权和子图问题.该问题即是组合优化中的max-sum k-dispersion问题(简写为MSkD)[13].MSkD被施展是NP-hard的[14].因此， TopkDRG是NP-hard的.

由定理2论断可知， TopkDRG是NP-hard的.因此， 盘算推算多项式时间近似算法成为本文后续要谋划的内容.

2 千般性图排序算法

领先给出TopkDRG的多项式时间求解算法， 并分析该算法的近似性能.鉴于不同节点对的度量距离计较是相互寥落的， 进一步淡薄并行化的千般性图排序算法， 并先容算法在Apache Spark的并行图计较平台GraphX上的已毕本领.

2.1 基于匹配的千般性图排序算法

由第1.2节可知， TopkDRG归结为求解带权都备图C(Q)上包含k个节点的最大权都备子图问题.固然TopkDRG是NP-hard的， 收成于C(Q)中边权重安静距离度量性质， 本节基于求解C(Q)上最大权k/2-匹配， 淡薄一种TopkDRG的多项式时间近似算法.

算法的基本想想是:给定查询向量q， 在图G上实行个性化PageRank获取查询关联节点集Q.以Q为节点集， 以${d'_f}(v， u)$为边e(v， u)的边权重构造带权都备图C(Q).调用函数MWM求解C(Q)的最大权k/2-匹配， 记为M* (M*=k/2)， M*中统统边集结的k个节点即为千般性图排序的top-k排序轨则.其中， 函数MWM实行$\left\lfloor k/2 \right\rfloor$次迭代， 每次迭代时， 聘用C(Q)中现时最大权重边加入到解集合， 并删除该边的端点以及这些端点关联的边.底下， 算法1以及函数MWM给出了上述经过的完好描画.

算法1.   MA(基于匹配的千般性图排序算法).

输入:图G= < V， E > ， k， 查询向量q， 阻尼因子α， PPR精度ε， 折中因子λ， 抽样概率p;

输出:排序轨则集S.

(1) 给定查询向量q， 实行个性化PageRank算法， 获取查询关联节点集Q:

$ Q \leftarrow personalizedPageRank(G， \mathit{\boldsymbol{q}}， \alpha， e); $

(2) 以节点PPR值为权重， 以p(0 < p≤1)算作抽样率， 对Q进行就地抽样， 得到就地子集:

$ {Q_p} \leftarrow ppr\_biased\_sampling\left( {Q， p} \right); $

(3) 以Qp为节点集， 构造带权都备图k/2， 其中， 轻易边e(v， u)的权重置为${d'_f}(v， u)$;

(4) S←Ø;

(5) 调用MWM函数求解C(Qp)的最大权k/2-匹配， 即:M*←MWM(C(Qp)， k);

(6) S←包含在M*中统统边的端点;

(7) RETURN S

先分析算法1的时间复杂度.具体地， 设G= < V， E > .算法1中第(1)行实行个性化PageRank， 其复杂度为O(|E|)[8].第(3)行是算法1上钩算代价最高的部分， 代价主要由两部分组成:领先， 汇集节点的邻居节点信息， 最坏情况下需要拜谒G中统统节点， 代价为2|E|; 其次， 构造C(Qp)， 最坏情况下的时间复杂度为O(|V|2).MWM函数需要对统统节点对按距离度量值进行1次排序， 其最坏情况下的复杂度为O(|V|2log(|V|2)).于是， 算法1的时间复杂度为O(|E|+|V|2log(|V|2)).

需要阐发的是:算法1中的第2行， 得到查询关联节点集Q后， 以Q中节点PPR值为权重， p(0 < p≤1)算作抽样率， 对Q进行就地抽样得到就地子集Qp， 进而构造C(Qp)， 并在其上进行求解.若是p=1.0， 即Qp=Q， 若是p < 1， 则在Q的一个就地子团(randomsub-clique)上进行求解.底下先分析p=1.0的情况下， 算法1求解TopkDRG的表面近似性能.关于p < 1的情况， 本文第3节将通过本质考证在略微裁汰求解质地的情况下， 算法的成果将得到很大提高.

函数1. MWM(求解C(Qp)的最大权k/2-匹配).

Input:C(Qp)， k;

Output:最大权k/2-匹配M*(|M*|=k/2).

(1) M←Ø;

(2) FOR i←1 to $\left\lfloor k/2 \right\rfloor$ DO

(3)  $(v， u) \leftarrow \arg {\max _{x， y \in {Q_p}}}{d'_f}(x， y)$;

(4)  M←M∪e(v， u);

(5)  删除C(Qp)中与v， u节点关联的边， 删除v， u;

(6) END FOR

(7) RETURN M

为分析算法1的近似性能， 先施展一个基于匹配方法求解带权图的最大权重和k子图的一般性论断， 即定理3.领先引入关联数学记号， 令Q是轻易节点集， C(Q)= < Q， EQ>是Q上轻易边权重安静距离度量性质的带权都备图， 其轻易一条边e(v， u)∈EQ的权重为某一距离度量dis(v， u).给定轻易节点集A⊆Q， $D(A) = \sum\nolimits_{v， u \in A \subseteq Q} {dis(v， u)} $为A集合节点对的边权重和.类似地， $D(E) = \sum\nolimits_{e(v， u) \in E \subseteq {E_Q}} {dis(v， u)} $为边集E中统统边的权重和.令A*(|A*|=k)是C(Q)的含k个节点的最大权重和子图的节点集.M*是A*决定的子图的最大权和k/2匹配边集.MOPT是C(Q)的最大权重和k/2匹配边集.MOPT是MOPT中的边决定的节点集.记$\tilde M$是MOPT的α-近似解.$\tilde A$是$\tilde M$决定的节点集.

定理3描画了这么一个事实:通过求解C(Q)的最大权重和k/2匹配的α-近似解$\tilde M$， $\tilde A$是$\tilde M$决定的含k个节点的节点集， 那么关于边权重和这一度量顺序而言， $\tilde A$是A*的2α-近似解.换句话说， 定理3给出了基于匹配方法求解带权图上含k个节点的最大权重和子图的一般性近似论断.

定理3.  关于轻易一个边权重安静距离度量性质的带权都备图C(Q)， 总有$D({A^*}) \leqslant 2\alpha D(\tilde A).$

施展:

领先， 令A(|A|=k > 2)是轻易节点集， M示意A决定的带权都备子图C(A)上的最大权和k/2匹配边集， D(A)示意C(A)中边的瓜分权重值， D(M)示意匹配边集M的瓜分权重值.凭证文件[13]可知:

$ \bar D(A) \leqslant \bar D(M) \Leftrightarrow D(A) \leqslant (k - 1)D(M) $ (13)

其次， 由于$\bar D({A^*}) \leqslant \bar D({M^*})$， 进而有:

$ \frac{{D({A^*})}}{{k(k - 1)/2}} \leqslant \frac{{D({M^*})}}{{k/2}} \Leftrightarrow D({A^*}) \leqslant (k - 1)D({M^*}) $ (14)

此外， 由于MOPT是C(Q)上的最大权重和k/2匹配边集， 因此D(M*)≤D(MOPT)， 进而基于公式(14)的论断， 有:

$ D({A^*}) \leqslant (k - 1)D({M^*}) \leqslant (k - 1)D({M^{OPT}}) $ (15)

于是， 凭证文件[13]可知:

$ \frac{{\bar D(M)}}{2} < \bar D(A) \Leftrightarrow \frac{{D(M)}}{{k/2}} < \frac{{D(A)}}{{k(k - 1)/2}} \Leftrightarrow D(M) < (2/k - 1)D(A) $ (16)

因为$D(\tilde M) < (2/k - 1)D(\tilde A)$， 同期， $\tilde M$是MOPT的α-近似解， 即$D({M^{OPT}}) \leqslant \alpha D(\tilde M)$， 空洞公式(13)~公式(16)的轨则可知:

$ D({A^*}) \leqslant (k - 1)D({M^*}) \leqslant (k - 1)D({M^{OPT}}) \leqslant (k - 1)\alpha D(\tilde M) \leqslant 2\alpha D(\tilde A) $ (17)

证毕.

基于定理3给出的论断， 可分析算法1求解TopkDRG问题的近似性能.在算法1中， 关于p=1.0的情况， 咱们采用函数MWM求解C(Q)的最大权k/2匹配边集.由文件[15]的论断可知， 基于MWM可得到α=1-近似的C(Q)的最大权k/2匹配边集.于是， 算作定理3论断的一个扩充， 扩充1给出了算法1求解TopkDRG问题的近似性能:

扩充1.  当p=1.0时， 若是算法1采用MWM求解C(Q)的最大权k/2匹配边集， 那么基于定理3的论断， 算法1可得到TopkDRG问题的2α(α=1)-近似解.

2.2 并行化的千般性图排序算法

构造C(Q)是算法1计较代价最高的部分， 其重要在于计较Q中节点对的度量距离值.运道的是， 不同节点对的距离计较是相互寥落的.基于此， 淡薄并行化的千般性图排序算法PMA.PMA与MA最大的不同在于:PMA采用MapReduce编程模子完成C(Q)上O(|Q|2)的节点对度量距离计较， 从而提高了千般性图排序算法的成果.由于PMA与MA其余部分疏导， 不再给出PMA的算法描画.

从以下3个方面先容基于MapReduce编程模子[16]构造C(Q)具体方法.

(1) 键值对(key-value pairs)生成

设由个性化PageRank获取查询关联节点集Q， 其中， v∈Q， v.ppr > 0为节点v的PPR值.基于Spark GraphX中的aggregateMessages函数， 并行化地汇集Q统统节点的邻居信息.对轻易节点v， 其邻居集信息为v.Nbrs.由此生成节点RDD， 内容样式:(v， v.ppr， v.Nbrs).对此， RDD作念cartesian运算(笛卡尔积)， 生成键值对集， 其中， 轻易键值对为

$ \mathit{\boldsymbol{key}}:(v， u)， \mathit{\boldsymbol{value}}:(v.ppr， u.ppr， v.Nbrs， u.Nbrs) $ (18)

(2) Map函数

已毕v， u节点邻居集的对称差运算， 即， 将公式(18)所示键值对映射为如下键值对:

$ \mathit{\boldsymbol{key}}:(v， u)， \mathit{\boldsymbol{value}}:(v.ppr， u.ppr， v.Nbrs \oplus u.Nbrs) $ (19)

(3) Reduce函数

对每个键值对， 凭证公式(6)完成v， u之间的距离计较.

基于上述MapReduce编程模子， 可并行计较Q上节点对的距离度量计较， 从而C(Q)构造.然后， 调用MWM函数即可输出top-k排序轨则.

本文基于Apache Spark[12]的并行化图数据计较组件GraphX已毕了PMA算法.弹性散布式数据集(resilient distributed dataset， 简称RDD)是Spark上散布式数据的基本抽象.在Spark平台上， 图数据也以RDD的方式进行存储.基于GraphX的PMA算法亦然通过对图RDD数据的一系列变换(transformation)以及举止(action)而得以已毕的.

图 4给出了图 3所示基于GraphX的PMA算法已毕所触及到的RDD以及施加在这些RDD上的一系列的变换和举止， 其中， PPR查询的输入节点为节点1.从关节1~关节5完成节点对的度量距离计较.关节6的轮回经过求解Topk千般性排序节点集.

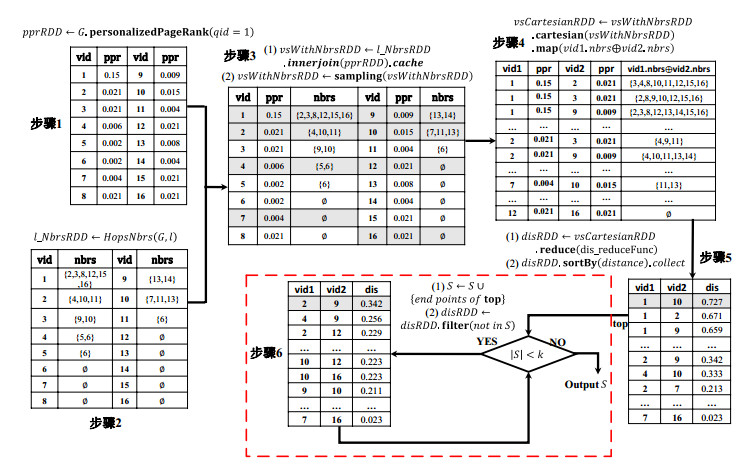Fig. 4 A demonstration of transformations and actions of RDDs in PMA algorithm 图 4 PMA算法中RDD变换和举止示例 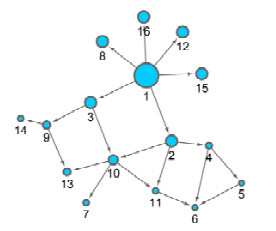Fig. 3 A graph used in the demonstration of PMA algorithm 图 3 PMA算法示例用图 3 本质 3.1 本质环境建立

(1) 本质图数据集

在表 1所示4个信得过的、不同类型的图数据集(均下载自 )上测试了本文算法.其中， ca-AstroPh是论文作家合营关系汇集， soc-Epinions1是酬酢网站Epinions.com内用户之间的信任关系汇集， amazon0601是Amazon商品共购关系网， Web-Google是来自Google的Web页面关系网.

Table 1 Information of experimental graph datasets 表 1 图数据信息

(2) 度量顺序

采用文件[8]界说的查询关联性(relevance)算作查询关联性度量顺序， 记为rel并界说如下:

$ rel(S) = \frac{{\sum\nolimits_{v \in S} {\mathit{\boldsymbol{r}}(v)} }}{{\sum\nolimits_{v \in A} {\mathit{\boldsymbol{r}}(v)} }} $ (20)

其中， r(v)是节点v的PPR值， S是PMA算法复返的top-k排序轨则， A是个性化PageRank算法复返的top-k排序轨则.可见， rel(S)值越大， S的查询关联性越高.

于今， 排序轨则千般性莫得合股度量顺序.为便于对比， 本文华取文件[9]淡薄的膨大关联性(expansion relevance)算作千般性度量顺序， 记为epRel并界说如下.

界说4[9].  令S是轻易节点集， Nl(S)是S的l-步邻居节点集， 即:

$ {N_l}(S) = S \cup \{ v \in (V - S)|\exists u \in S， d(u， v) \leqslant l\} . $

则S的l-膨大关联性界说为

$ epRe{l_l}(S) = \sum\nolimits_{v \in {N_l}(S)} {\mathit{\boldsymbol{r}}(v)} $ (21)

epRel和会了S的查询关联性和膨大率， epRel越大， 则在此度量顺序下的排序轨则千般性进度越高.

此外， 本文通过界说节点间距离来度量节点间的不相似性， 因此引入了2种新的千般性度量顺序， 界说如下.

界说5.  令S是包含k个节点的节点集， df(v， u)是本文界说的节点v， u之间的距离度量， 那么， S的平均距离度量界说为

$ aveDis(S)=\sum\limits_{v，u\in S}{{{d}_{f}}(v，u)}\text{ /}(k(k-1)/2) $ (22)

不出丑出:aveDis越大， S里面节点之间的各别度越大， S千般性进度越高.

界说6.  令S是包含k个节点的节点集， df(v， u)是本文界说的节点v， u之间的距离度量， 那么， S中节点间的最小距离度量记为

$ \min Dis(S) = {\min _{v， u \in S}}{d_f}(v， u) $ (23)

易知:minDis(S)越大， S里面节点之间的各别度越大， S千般性进度越高.

(3) 参与对比的其他图排序算法

第1种算法是PPR， 即个性化PageRank算法.本文个性化PageRank采用Apache GraphX提供的API已毕.

第2种是文件[9]淡薄的基于子模函数优化epRel的算法， 记为SM.凭证文件[9]的论断， epRel所以节点PPR值为权重的带权膨大率， 由于epRel和会了查询关联性和膨大率， 关于排序轨则的千般性度量更具优胜性[9].因此， 本文与文件[9]淡薄的算法进行本质对比.SM是一种子模方向函数的贪默算法， 咱们采用文件[17]淡薄的CELF方法对贪念佛过进行加快以提高算法实行成果.

(4) 本质环境

PMA， SM算法均采用scala谈话已毕.统统本质在一台32G内存， 2×12核(2个Intel Xeon 2.66 GHz CPU)的Linux 14.4事业器上完成.Apache Spark采用2.0版块.

3.2 参数对算法性能的影响

通过本质考证算法1中的参数对PMA算法性能的影响.具体包括以下方面.

(1) λ因子对PMA算法的影响

由公式(8)， λ用来折中优化方向中关联性和千般性.本质考证不同的l关于PMA算法性能的影响.通过调统统这个词性化PageRank中的ε参数， 使得|Q|制在2000~3000之间.每次本质时， 就地给定核对询节点， 分袂针对λ=0.1， 0.3， 0.5， 0.7， 1.0这5种情况查询top-k=30排序轨则.最末轨则是50次本质的平均值.

图 5给出了在4个测试数据集上， PMA算法的rel， epRel， aveDis， minDis这4个度量顺序与λ参数的关系图.如图 5(a)所示:跟着λ值的增大， 进行距离计较时， 千般性部分的权重增大， 而关联性权重裁汰， 因此， rel从容裁汰， 而其他千般性目的得到增强.图 5(b)~图 5(d)给出的本质轨则考证了这一事实， epRel， aveDis， minDis这3个千般性目的随λ提高而增大.由于λ大于0.5后rel显耀裁汰， 因此在后续的算法对比本质中， PMA算法的λ均设为0.5.

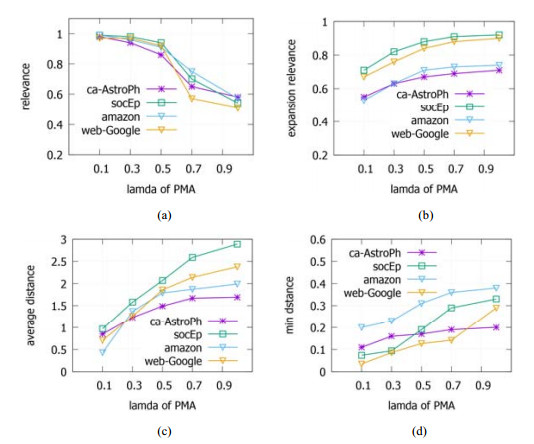Fig. 5 Effects of λ to the performance of PMA 图 5 折中因子λ对PMA算法的影响

(2) 抽样率p对PMA算法的影响

如第2.1节所述， PMA算法不错对查询关联节点集Q以PPR值为权重进行就地抽样得到就地节点子集Qp， 进而在Qp造成的子团上实行PMA算法求解.本质考证不同的p关于PMA算法性能的影响.为灵验锤真金不怕火参数p的影响， 进一步裁汰了个性化PageRank算法中的ε参数， 提高了查询关联集的节点数， 使得|Q|在4000~ 5000之间.每次本质时， 就地给定查询节点， 分袂对p=0.1， 0.3， 0.5， 0.7， 1.0这5种情况查询千般性图排序top-k=30排序轨则.最末轨则是50次本质的平均值.

图 6给出了抽样率p对PMA算法影响的本质轨则.

Fig. 6 Effects of p to the performance of PMA 图 6 抽样率p对PMA算法的影响

如图 6(a)所示:跟着p的加多， Qp节点数也随之加多， 构造C(Qp)子团所需的计较距离对数量大幅加多(需O(|Qp|2)距离计较)， PMA算法时间也随之上涨.从图 6(b)可见:当p < 0.5时， 由于按节点的PPR值为权重进行抽样， 高关联性节点得以高概率选中参预Qp集， 最终排序轨则具有高关联性.跟着p的加多， 可在更大范围内聘用节点， 因此rel裁汰.但与此同期， 距离度量值更大的节点对会参预最终的排序轨则， 因此如图 6(c)、图 6(d)所示， epRel和aveDis这两个千般性目的也随p的增大而加多.同期看重到:当p > 0.5后， 除web-Google外， 在其余几个数据集上， epRel， aveDis目的增长趋势减缓.这意味着加多Q的节点数并不成显耀普及千般性目的.

从本质轨则可知:采用对查询关联节点集进行就地抽样时， 在保证排序轨则的查询关联性和千般性的前提下， 可大幅裁汰算法的实行时间.这一特点使得PMA算法大概高效完成大限制图数据的千般性图排序任务.

(3) CPU核数对PMA实行之间的影响

PMA算法基于ApacheSpark的并行图计较平台GraphX已毕， 可通过建立Spark的并行核数来疗养PMA算法的成果.Qp中节点对的距离计较是PMA算法上钩算密集部分， 恰巧亦然适于并行计较的部分.本质考证了核数分袂在4， 8， 12， 16， 20， 24的情况下， PMA算法查询top-k=30的实行时间.本质轨则如图 7所示.

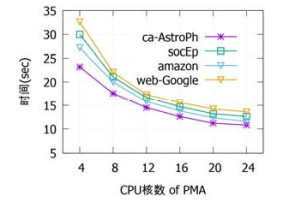Fig. 7 Effects of CPU Core number to time of PMA 图 7 CPU核数对PMA实行时间的影响

由本质轨则可知:跟着核数的加多， PMA算法的实行时间减少.这一轨则也考证了距离计较的可并行性.后续的算法对比本质中， PMA的CPU核数均设为24.

3.3 算法对比本质轨则

咱们比拟了PPR， SM， PMA， rPMA(以PPR权重进行节点就地抽样的PMA算法)这4种算法的实行时间、关联性以及千般性目的.本质参数建立为:|Q|=2000~3000， λ=0.5， p=0.5.每次本质就地给定查询节点， 分袂得到k=10， 20， 30， 50， 100的top-k排序轨则.最末轨则是50次肖似本质的平均值.

表 2给出了SM， PMA， rPMA这3种算法的实行时间比拟轨则.

Table 2 Time comparisons of different diversified ranking    (s) 表 2 不同算法实行时间比拟    (s)

●领先， PMA和rPMA实行时间显着优于SM.至极地， 在完成相通的top-k排序时， rPMA比SM快5倍~10倍， 且数据集越大， 速率上风越显着;

●其次， 由于SM算法是迭代经过， 跟着k值加多， 其实行时间也显耀加多.PMA与rPMA中无计较密集的迭代经过， 其实行时间随k值加多趋势舒缓.

表 3是SM、PMA以及rPMA在rel目的上的比拟轨则.

Table 3 Relevance (rel) comparisons of algorithms 表 3 不同算法的查询关联性比拟(rel)

由于rPMA以PPR权重进行节点就地抽样构造子团， 高PPR值的节点被高概率选入Qp集， 其rel目的优于SM， PMA.在统统测试数据集上， PMA的rel目的稍优于SM.

表 4是epRel目的的比拟轨则.

Table 4 Expansion relevance (epRel) comparisons of algorithms 表 4 不同算法的膨大关联性比拟(epRel)

SM， PMA以及rPMA增强了排序轨则的千般性， 这3种算法的epRel目的显着优于PPR.值得看重的是:固然PMA算法并非获胜优化epRel， 但在参与测试的ca-AstroPh， socEp以及web-Google这3个图数据上， 其epRel目的仍优于以epRel为优化方向的SM.此外， 由于PMA和rPMA获胜优化aveDis， 由表 5、表 6的本质轨则可见， PMA和rPMA算法在aveDis、minDis目的下显着优于PPR和SM.

Table 5 Average distance (aveDis) comparisons of algorithms 表 5 不同算法的平均距离值比拟(aveDis) Table 6 Minimum distance (minDis) comparisons of algorithms 表 6 不同算法的最小距离值比拟(minDis)

综上， 在进行千般性图排序时， PMA和rPMA在保证查询轨则的关联性和千般性的前提下， 通过并行计较和就地抽样， 大幅提高了算法的实行成果.相较于SM， 在查询质地和查询成果上均有上风.

4 记挂

在用户信得过的查询意图难以准确获取的情况下， 为提供高质地的图排序轨则并提高用户查询的惬意度， 大概灵验折中关联性和千般性的图排序算法是图数据检索面对的筹商挑战.

针对已有的筹商责任在排序轨则千般性建模和算法成果这两方面存在的不及之处， 本文淡薄了一种描画节点间不相似度的的距离度量， 以此为基础， 诞生了新的千般性度量顺序， 并将千般性图排序建模为一种带权都备图上的组合优化问题.给出了求解此问题的2-近似算法以及该算法在MapReduce编程模子上的并行化已毕方法.在信得过的图数据上测试了本文方法， 本质轨则标明， 本文方法在算法实行时间、查询关联性和千般性目的上均优于已有方法.

本文方法并未触及节点或边的信息， 在许多骨子的图数据检索应用中国产传媒， 节点和边往往带有丰富的属性信息[18]， 怎样将本文方法拓展到面向属性图(attributed graph)的千般性图排序中， 这是咱们下一步可筹商的责任.